Lý thuyết Trò chơi (Game Theory) là một lĩnh vực của toán học ứng dụng, nghiên cứu về cách mà các cá nhân hoặc tập thể đưa ra quyết định trong một tình huống tương tác và ảnh hưởng lẫn nhau. Nó tập trung vào việc mô hình hóa, phân tích và dự đoán các kết quả của các trò chơi hoặc tình huống tương tác với sự tham gia của các người chơi có một số lượng hữu hạn các lựa chọn.
Lý thuyết Trò chơi đã có những đóng góp quan trọng trong nhiều lĩnh vực, từ kinh tế học, chính trị học, tâm lý học cho đến công nghệ thông tin và kỹ thuật. Nó đã giúp chúng ta hiểu được cách mà các cá nhân hoặc tổ chức tương tác với nhau, dự đoán và đưa ra quyết định trong một tình huống phức tạp, đồng thời cũng cung cấp cho chúng ta những công cụ và phương pháp để tối ưu hóa quyết định của mình.
Trong bối cảnh ngày nay, khi các vấn đề xã hội, kinh tế và chính trị ngày càng phức tạp, lý thuyết Trò chơi trở nên càng quan trọng hơn bao giờ hết. Nó cung cấp cho chúng ta một cách nhìn đa chiều về thế giới xung quanh và giúp chúng ta đưa ra những quyết định đúng đắn và hiệu quả trong mọi lĩnh vực của cuộc sống.
Trong bài viết này hãy cùng CryptoViet tìm hiểu về chủ đề này nhé!
Lý thuyết trò chơi là gì?
Lý thuyết Trò chơi (Game Theory) là một lĩnh vực nghiên cứu toán học liên quan đến việc phân tích và mô hình hóa các tình huống tương tác giữa các cá nhân hoặc tổ chức, được gọi là “người chơi” (players) trong lý thuyết này. Trong các tình huống này, các người chơi có thể có lợi ích riêng hoặc chung, và sẽ đưa ra quyết định dựa trên một loạt các thông tin và giả định về hành vi của những người chơi khác.
Lý thuyết Trò chơi xuất hiện lần đầu vào đầu thế kỷ 20, khi các nhà toán học như John von Neumann và Oskar Morgenstern đã bắt đầu phát triển các phương pháp phân tích cho các tình huống tương tác trong kinh tế và chính trị. Tuy nhiên, lý thuyết Trò chơi cũng có ứng dụng rộng rãi trong các lĩnh vực khác như khoa học xã hội, kỹ thuật, công nghệ thông tin và sinh học.
Các tình huống trong lý thuyết Trò chơi có thể được mô hình hóa bằng cách sử dụng các cấu trúc toán học như ma trận và đồ thị. Mỗi tình huống có thể có một hoặc nhiều người chơi, mỗi người chơi sẽ đưa ra một hành động, và kết quả của tình huống sẽ phụ thuộc vào những hành động đó. Những kết quả này có thể được biểu thị bằng một bảng thanh toán (payoff matrix), nơi mà mỗi ô trong bảng đại diện cho kết quả tương ứng với một cặp hành động từ hai người chơi khác nhau.
Một trong những khái niệm quan trọng trong lý thuyết Trò chơi là khái niệm “định lý Nash” (Nash equilibrium), được đặt theo tên của nhà toán học John Nash, người đã đưa ra khái niệm này vào năm 1950. Định lý Nash mô tả một trạng thái tương ứng với một bộ hành động của các người chơi, trong đó không ai muốn thay đổi hành động của mình khi biết hành động của người chơi khác. Đây được coi là một trạng thái cân bằng của tình huống, nơi mà không có ai có thể tăng lợi ích của mình bằng cách thay đổi hành động của mình. Định lý Nash được xem là một trong những khái niệm quan trọng nhất của lý thuyết Trò chơi và đã được áp dụng rộng rãi trong nhiều lĩnh vực.
Các tình huống trong lý thuyết Trò chơi có thể được chia thành hai loại: tình huống không hợp tác (non-cooperative game) và tình huống hợp tác (cooperative game). Trong tình huống không hợp tác, các người chơi đưa ra quyết định dựa trên lợi ích cá nhân của mình mà không có sự hợp tác hoặc thỏa hiệp nào giữa các người chơi. Trong tình huống hợp tác, các người chơi có thể thỏa thuận với nhau để đạt được kết quả tốt hơn cho tất cả mọi người.
Lý thuyết Trò chơi có nhiều ứng dụng trong thực tế, từ kinh tế, chính trị đến khoa học xã hội. Ví dụ, nó được sử dụng để giải quyết các vấn đề trong quản lý tài sản, tài chính và đầu tư, cũng như để phân tích các chiến lược trong các lĩnh vực như quân sự, thương mại và đàm phán. Nó cũng được sử dụng để nghiên cứu các hệ thống tự động và trí tuệ nhân tạo.
Trong những năm gần đây, lý thuyết Trò chơi đã trở thành một trong những công cụ quan trọng trong phân tích dữ liệu và khoa học dữ liệu. Nó được sử dụng để tìm kiếm các mô hình phân tích dữ liệu và để giải quyết các vấn đề như định giá sản phẩm, dự đoán hành vi người dùng và tối ưu hóa quảng cáo trực tuyến.
Song đề tù nhân
Song đề tù nhân hay Thế tiến thoái lưỡng nan của người tù (Prisoner’s Dilemma) là một trò chơi trong lý thuyết trò chơi với tổng không bằng không. Song đề này được phát biểu một cách đơn giản như sau:
| B không khai | B thú tội | |
| A không khai | Cả hai được thả | A được tự do. B bị chung thân. |
| A thú tội | B được tự do. A bị chung thân. | Cả hai bị 10 năm tù. |
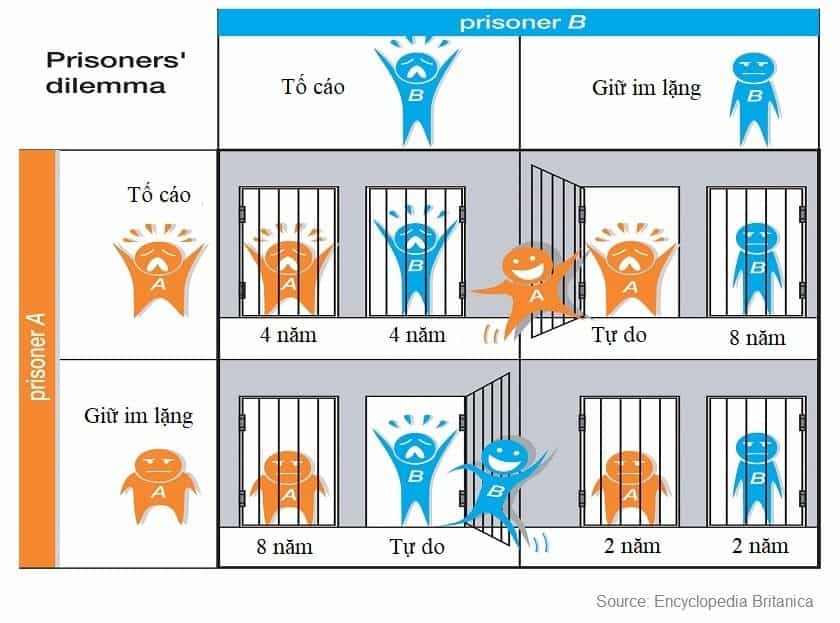
Giả sử A và B bị bắt gặp ăn cắp một cửa hàng tạp hóa và trong quá trình điều tra, cảnh sát đã phát hiện ra rằng cả hai đã phạm tội nghiêm trọng hơn nhiều trong quá khứ. Cảnh sát nghi ngờ cả hai người này đều dính líu đến một vụ cướp ngân hàng. Trong quá trình điều tra, cảnh sát thẩm vấn từng người một và đưa ra ba đề xuất như sau:
- Đề xuất thứ nhất: Nếu cả hai im lặng và không khai ra người còn lại thì cả hai sẽ cùng phải ngồi tù 2 năm do tội ăn cắp.
- Đề xuất thứ hai: Nếu một trong hai người khai ra người kia và người kia im lặng, thì người chịu khai ra sẽ được miễn án phạt và được thả tự do, trong khi người kia sẽ nhận án 8 năm tù.
- Đề xuất thứ ba: Nếu cả hai đều khai ra nhau thì mỗi người đều sẽ nhận 4 năm tù.
Trong trường hợp này, mỗi tù nhân có hai lựa chọn: hợp tác với kẻ còn lại và giữ im lặng, hay phản bội và khai ra kẻ còn lại. Kết quả của mỗi lựa chọn đều tuỳ thuộc vào lựa chọn của người kia. Tuy nhiên, không ai biết được lựa chọn của người kia. Nếu họ có thể nói chuyện với nhau, họ cũng chưa chắc là tin tưởng nhau được. Từ đó ta xây dựng được ma trận thưởng phạt như sau:

Giả sử có hai tù nhân A và B, cả hai đều ích kỷ và muốn giảm thiểu thời gian tù tội của mình. Nếu A tin rằng B sẽ giữ im lặng, thì lựa chọn tối ưu của A là đổ tội cho B, vì A sẽ được thả tự do ngay lập tức trong khi B sẽ phải ngồi tù 8 năm. Ngược lại, nếu A tin rằng B sẽ khai ra mình, thì lựa chọn tối ưu của A là đổ tội và khai ra tên của B, vì nếu A phản bội thì A sẽ bị tù chỉ 4 năm thay vì 8 năm nếu giữ im lặng. Tuy nhiên, nếu cả hai tù nhân hợp tác với nhau và giữ im lặng, thì cả hai sẽ được thả tự do trong vòng 2 năm.
Tuy nhiên, điều này đưa chúng ta đến một vấn đề. Nếu có một kịch bản mà giải pháp tối ưu cho cả hai tù nhân lại có tác động xấu đối với xã hội, thì điều gì sẽ xảy ra? Ví dụ, nếu A và B đang lên kế hoạch cho một vụ gian lận để tấn công tiền điện tử với ma trận thưởng phạt, trong trường hợp này, giải pháp tối ưu cho cả hai tù nhân có thể là không thực hiện vụ gian lận để tránh gây tổn hại cho xã hội. Tuy nhiên, với động cơ ích kỷ của cả hai, họ có thể quyết định tiếp tục lên kế hoạch cho vụ gian lận, dẫn đến hậu quả xấu cho xã hội.
Giả sử A và B đang lên kế hoạch cho một vụ gian lận để tấn công tiền điện tử với ma trận thưởng phạt trong trường hợp này như sau:
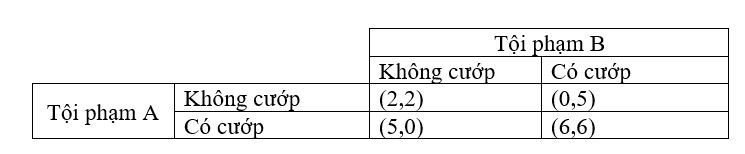
Như bạn có thể thấy, trong kịch bản giả thuyết này, chiến lược tốt nhất và tối ưu nhất xảy ra khi cả A và B đều gian lận để thực hiện vụ tấn công. Mặc dù điều này có thể tốt cho cả hai, nhưng nó không phải là điều tốt cho xã hội nói chung. Sở dĩ có điều này bởi trò chơi mà họ đang chơi là trò chơi luôn thắng, và không bị trừng phạt khi thua.
Vì vậy, để hạn chế sự gian lận, đây là lúc chúng ta đưa ra các ý tưởng trừng phạt cho các hành vi gian lận.
Trong ví dụ trên, giả sử chúng ta đưa ra một chiến lược trừng phạt như sau:
Sau mỗi lần công chúng bị thiệt hại -0,5 đơn vị lợi ích, kẻ gian lận sẽ bị trừng phạt -6 đơn vị lợi ích.
Nói cách khác, mọi hành động xấu đối với xã hội sẽ bị trừng phạt nghiêm khắc. Khi kẻ bị buộc tội gây ra thiệt hại -0.5 đơn vị lợi ích cho xã hội (về tiền bạc, thời gian,…) sẽ phải chịu trừng phạt gấp nhiều lần thiệt hại gây ra (-6 đơn vị lợi ích).
Khi thêm yếu tố trừng phạt cho các hành vi xấu, ma trận thưởng phạt sẽ có dạng như sau:
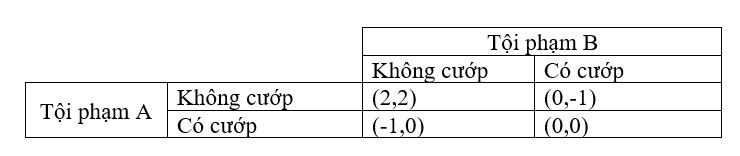
Thay vì thực hiện việc gian lận mà không bị trừng phạt, những kẻ phạm tội giờ đây phải đối mặt với những hậu quả nghiêm trọng hơn nhờ vào yếu tố trừng phạt được thêm vào. Như vậy, cân bằng Nash đã thay đổi từ một chiến lược có thể có hại cho xã hội sang một chiến lược tốt cho xã hội, và đây trở thành động cơ để các cá nhân tuân thủ đúng các giao thức xã hội.
Mặc dù có nhiều biến thể của song đề tù nhân, câu chuyện đơn giản này đã minh họa ý tưởng sử dụng các mô hình lý thuyết trò chơi để nghiên cứu hành vi của con người và các kết quả có thể có dựa trên quá trình ra quyết định hợp lý của con người.
Lý thuyết trò chơi trong crypto
Lý thuyết trò chơi được áp dụng rộng rãi trong lĩnh vực tiền điện tử và blockchain, được gọi là “lý thuyết trò chơi trong crypto” (game theory in crypto). Lý thuyết trò chơi giúp phân tích và dự đoán hành vi của các bên trong một mạng lưới tiền điện tử, đặc biệt là trong các hệ thống đồng thuận (consensus) và bảo mật.
Trong hệ thống đồng thuận, lý thuyết trò chơi được sử dụng để dự đoán hành vi của các thợ đào (miners) trong quá trình xác nhận giao dịch và tạo khối mới. Các thợ đào cạnh tranh để giành được phần thưởng (reward) bằng cách tìm ra một khối mới trước các thợ đào khác. Tuy nhiên, nếu tất cả các thợ đào cùng đào trên một khối, mạng sẽ bị chia tách và tạo thành hai phiên bản khác nhau của blockchain (fork). Do đó, các thợ đào phải quyết định đào trên khối nào để tạo ra một blockchain đồng nhất. Lý thuyết trò chơi giúp phân tích các chiến lược đào khác nhau và dự đoán kết quả của các tình huống khác nhau.
Ngoài ra, lý thuyết trò chơi cũng được sử dụng để nghiên cứu bảo mật của các mạng lưới tiền điện tử. Các tấn công bảo mật có thể được xem như một trò chơi giữa kẻ tấn công và hệ thống bảo mật. Lý thuyết trò chơi giúp dự đoán các chiến lược tấn công và tìm ra các chiến lược phòng thủ tốt nhất để đảm bảo an toàn cho hệ thống.
Ngoài ra, lý thuyết trò chơi còn được áp dụng trong các thị trường tiền điện tử, nơi các nhà đầu tư cạnh tranh để tìm ra các cơ hội đầu tư tốt nhất. Các nhà đầu tư cũng có thể áp dụng lý thuyết trò chơi để dự đoán tình hình thị trường và lựa chọn chiến lược đầu tư phù hợp.
Lời kết
Tóm lại, lý thuyết trò chơi đóng vai trò quan trọng trong việc phân tích và dự đoán các tình huống phức tạp trong lĩnh vực tiền điện tử và blockchain. Lý thuyết trò chơi cung cấp một cách tiếp cận khoa học để nghiên cứu hành vi của các đối tác trong một hệ thống phức tạp, giúp ta có thể dự đoán được các chiến lược và hành vi của các bên liên quan đến hệ thống.



Trả lời